Hunting Prime Numbers with Sieves
Posted onbyPreet Mishra · 0 views
Prime numbers are fascinating and have been a subject of curiosity from decades. The reason for their hype roots to the fundamental theorem of arithmetic which states that every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
Formally, a prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
In this post, we will go through a simple yet effective algorithm which is known as Sieve of Eratosthenes to find all the prime numbers below a given limit.
The reason we are interested in this particular algorithm is because of its efficiency in terms of time complexity which is O(nloglogn). In fact, It is the most effective algorithm for finding prime numbers up to 10 million.
Algorithm
- Create a list of integers from 2 to n.
- Start with p being equal to 2, the smallest prime number.
- Mark the multiples of p starting from p * p up to n one by one, the p itself should not be marked.
- Find the first number greater than p in the list that is not marked. If there is no such number, stop. Otherwise, set p equal to this new number, and repeat from step 3.
- When the algorithm terminates, the numbers which are not marked in the list are all the primes below n.
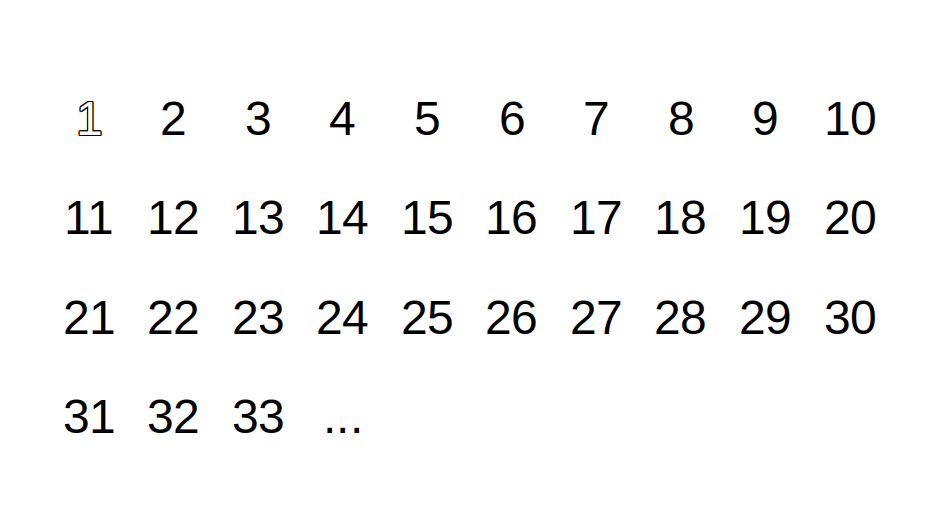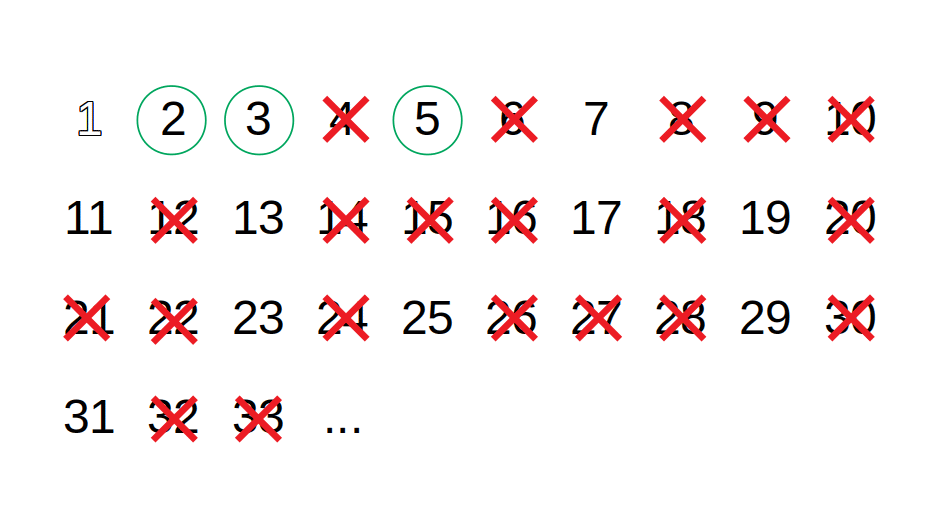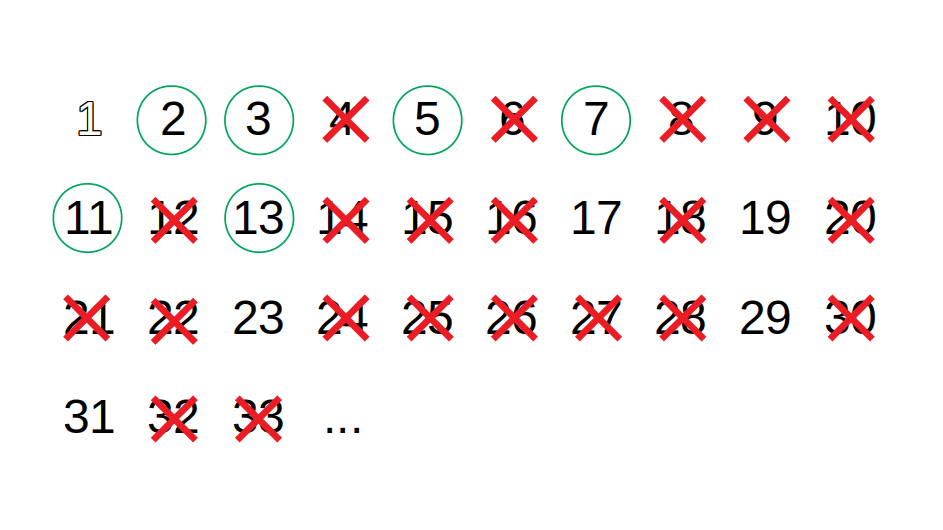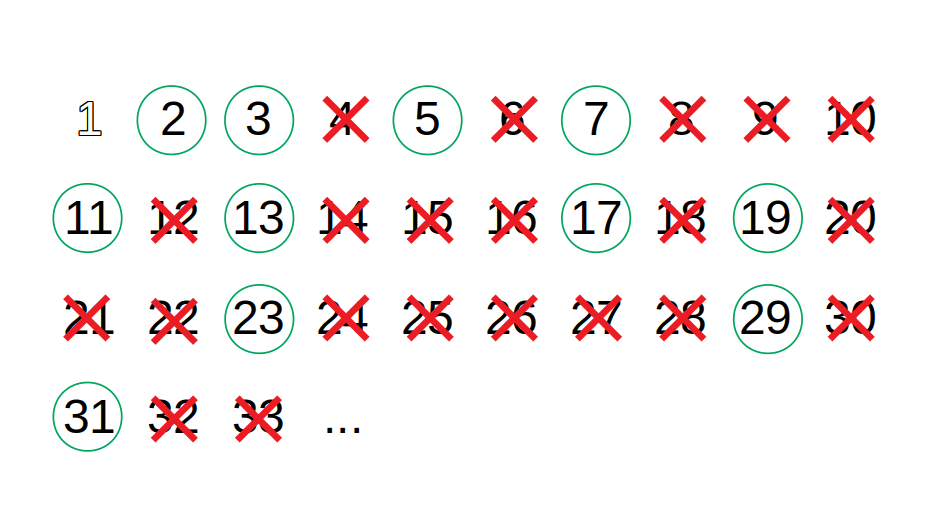
Implementation
def sieves(n):
primes = [1] * n
primes[0] = primes[1] = 0
total = 0
p = 2
while p * p <= n:
if p:
i = p * p
while i < n:
primes[i] = 0
i += p
p += 1
primes = [i for i, j in enumerate(primes) if j]
return primes
This is a straight forward implementation of the algorithm. Here, we initialize all the indices up to n with 1(True) except 0 and 1 as they are not prime numbers. Next, we iterate for every number which has not been marked(has 1(True)) and set(mark) its multiples to 0(False) starting. Notice we start marking the multiples after the square of p to avoid marking the numbers which already have been marked. When the outer loop terminates, we obtain our prime numbers.
Optimization
As we know that the only even prime number we have is 2 so we don't need to deal with even numbers as all they are doing is taking space in our array. So the idea is to only apply sieves to odd numbers to find primes and add 2 in the end. Turns out with a little bit of simple index arithmetic we can easily optimize our previous implementation. Since we will be only dealing with odd numbers, we will treat index i as number (2 * i) + 1. For instance, index 1 will be treated as number 3. Consequently, the square of the number at index i will be at index (2 * i) * (i + 1) and the step to be taken in the inner loop will be (2 * i) + 1.
def sieves(n):
if n < 2:
return []
n = n // 2
primes = [1] * n
primes[0] = 0
i = 1
while (2 * i) * (i + 1) <= n:
if i:
j = (2 * i) * (i + 1)
while j < n:
primes[j] = 0
j += (2 * i) + 1
i += 1
primes = [(2 * i) + 1 for i, j in enumerate(primes) if j]
primes.insert(0, 2)
return primes